Dois atletas correm com velocidades constantes em uma pista retilínea, partindo simultaneamente de extremos opostos, A e B. Um dos corredores parte de A, chega a B e volta para A. O outro corredor parte de B, chega a A e volta para B. Os corredores cruzam-se duas vezes, a primeira vez a 800 metros de A e a segunda vez a 500 metros de B. O comprimento da pista, em metros, é
Considerando 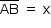 , a questão pode ser dividida em 2 partes:
, a questão pode ser dividida em 2 partes:
1º) Os atletas correm até o ponto M:

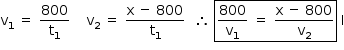
2º) Os atletas partem de M e correm até N, respeitando a volta.

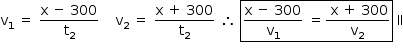
De I e II, tem-se: