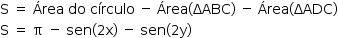O quadrilátero da figura está inscrito em uma circunferência de raio 1. A diagonal desenhada é um diâmetro dessa circunferência.
Sendo x e y as medidas dos ângulos indicados na figura, a área da região cinza, em função de x e y, é:
- a
π + sen(2x) + sen(2y)
- b
π - sen(2x) - sen(2y)
- c
π - cos(2x) - cos(2y)
- d
- e
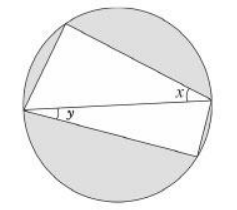
Seja ABCD o quadrilátero inscrito no círculo de diâmetro AC = 2.
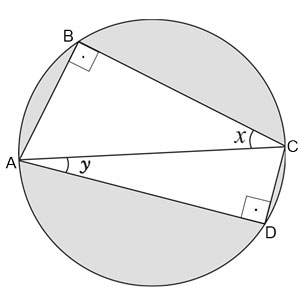
Os triângulos ABC e ADC são retângulos de mesma hipotenusa AC. Nessas condições, tem-se:
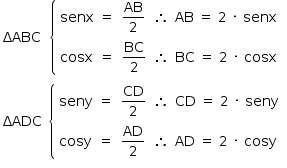
Calculando as áreas, tem-se:
Área do círculo = π · 12 = π
Portanto, chamando de S a área da região cinza pedida, tem-se:
