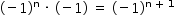Considere o polinômio
em que a0, ... , an-1 ∈ ℝ. Sabe-se que as suas n raízes estão sobre a circunferência unitária e que a0 < 0.
O produto das n raízes de P(x), para qualquer inteiro n ≥ 1, é:
Considerando que a circunferência unitária está centrada na origem, tem-se que as n raízes complexas de P(x) têm módulo igual a 1. Denotando essas n raízes por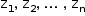 
, pelas relações de Girard, seu produto é:
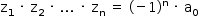
Aplicando o módulo a ambos os membros da igualdade e levando em conta que o módulo do produto é igual ao produto dos módulos, tem-se:
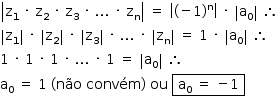
Assim, o produto das raízes é igual a 