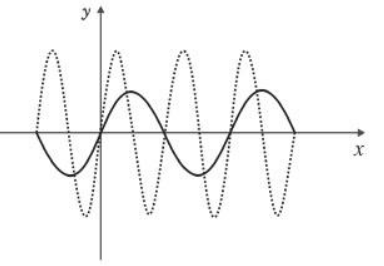
Admitindo que a linha pontilhada represente o gráfico da função ƒ(x) = sen(x) e que a linha contínua represente o gráfico da função g(x) = αsen(βx), segue que
Pelo gráfico, observa-se que o período da função g(x) (Tg) é o dobro do período da função f(x) (Tf).
Como 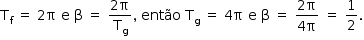
Logo, 
Como, também pelo gráfico, a amplitude da função g(x) é menor que a da função f(x), então 0 < α < 1.