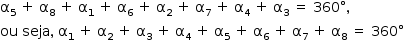Prolongando-se os lados de um octógono convexo ABCDEFGH, obtém-se um polígono estrelado, conforme a figura.
A soma α1 + ••• + αB vale
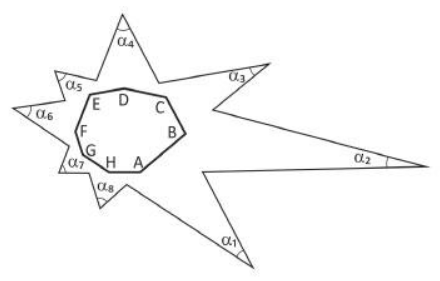
Considere a figura a seguir, com os pontos e as medidas assinaladas:
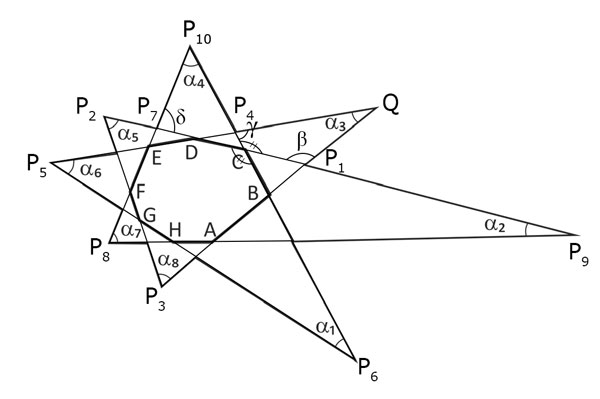

De (I), (II), (III), (IV) e (V), tem-se:
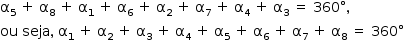
Prolongando-se os lados de um octógono convexo ABCDEFGH, obtém-se um polígono estrelado, conforme a figura.

A soma α1 + ••• + αB vale
Considere a figura a seguir, com os pontos e as medidas assinaladas:


De (I), (II), (III), (IV) e (V), tem-se: