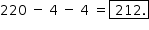Doze pontos são assinalados sobre quatro segmentos de reta de forma que três pontos sobre três segmentos distintos nunca são colineares, como na figura.
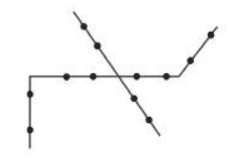
O número de triângulos distintos que podem ser desenhados com os vértices nos pontos assinalados é
Pode-se escolher 3 pontos dentre os 12, de 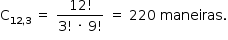
Porém, como em dois dos quatro segmentos há 4 pontos colineares, deve-se excluir os casos em que essas três escolhas são feitas a partir desses três pontos.
Isso pode ser feito de 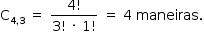
Logo, o total de triângulos que podem ser desenhados é