Anglo Resolve

Questão 24

Em uma urna, há bolas amarelas, brancas e vermelhas. Sabe-se que:

I. A probabilidade de retirar uma bola vermelha dessa urna é o dobro da probabilidade de retirar uma bola amarela.

II. Se forem retiradas 4 bolas amarelas dessa urna, a probabilidade de retirar uma bola vermelha passa a ser 1/2.

III. Se forem retiradas 12 bolas vermelhas dessa urna, a probabilidade de retirar uma bola branca passa a ser 1/2.

A quantidade de bolas brancas na urna é

a
8.
b
10.
c
12.
d
14.
e
16.

Resolução

Considerem-se A, B e V, respectivamente, as quantidades de bolas amarelas, brancas e vermelhas na urna,

Da informação I, tem-se que
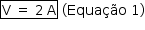
Da informação II, tem-se, ao retirar 4 bolas amarelas, as bolas vermelhas passam a representar metade das restantes, que são (A – 4) + B + V. Assim:

$«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨14px¨»«mi mathvariant=¨normal¨»V«/mi»«mo»§#xA0;«/mo»«mo»=«/mo»«mo»§#xA0;«/mo»«mfrac»«mn»1«/mn»«mn»2«/mn»«/mfrac»«mfenced open=¨[¨ close=¨]¨»«mrow»«mfenced»«mrow»«mi mathvariant=¨normal¨»A«/mi»«mo»§#xA0;«/mo»«mo»-«/mo»«mo»§#xA0;«/mo»«mn»4«/mn»«/mrow»«/mfenced»«mo»§#xA0;«/mo»«mo»+«/mo»«mo»§#xA0;«/mo»«mi mathvariant=¨normal¨»B«/mi»«mo»§#xA0;«/mo»«mo»+«/mo»«mo»§#xA0;«/mo»«mi mathvariant=¨normal¨»V«/mi»«/mrow»«/mfenced»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#x2234;«/mo»«mo»§#xA0;«/mo»«menclose notation=¨box¨»«mi mathvariant=¨normal¨»V«/mi»«mo»§#xA0;«/mo»«mo»=«/mo»«mo»§#xA0;«/mo»«mi mathvariant=¨normal¨»A«/mi»«mo»§#xA0;«/mo»«mo»+«/mo»«mo»§#xA0;«/mo»«mi mathvariant=¨normal¨»B«/mi»«mo»§#xA0;«/mo»«mo»-«/mo»«mo»§#xA0;«/mo»«mn»4«/mn»«/menclose»«mo»§#xA0;«/mo»«mo»(«/mo»«mi»Equa§#xE7;§#xE3;o«/mi»«mo»§#xA0;«/mo»«mn»2«/mn»«mo»)«/mo»«/mstyle»«/math»$

Da informação III, tem-se, ao retirar 12 bolas vermelhas, as bolas brancas passam a representar metade das restantes, que são A + B (V – 12). Assim:

$«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨14px¨»«mrow»«mi mathvariant=¨normal¨»B«/mi»«mo»§#xA0;«/mo»«mo»=«/mo»«mo»§#xA0;«/mo»«mfrac»«mn»1«/mn»«mn»2«/mn»«/mfrac»«mo»§#xA0;«/mo»«mfenced open=¨[¨ close=¨]¨»«mrow»«mi mathvariant=¨normal¨»A«/mi»«mo»§#xA0;«/mo»«mo»+«/mo»«mo»§#xA0;«/mo»«mi mathvariant=¨normal¨»B«/mi»«mo»§#xA0;«/mo»«mo»+«/mo»«mo»§#xA0;«/mo»«mfenced»«mrow»«mi mathvariant=¨normal¨»V«/mi»«mo»§#xA0;«/mo»«mo»-«/mo»«mo»§#xA0;«/mo»«mn»12«/mn»«/mrow»«/mfenced»«/mrow»«/mfenced»«mo»§#xA0;«/mo»«mo»§#xA0;«/mo»«mo»§#x2234;«/mo»«mo»§#xA0;«/mo»«menclose notation=¨box¨»«mi mathvariant=¨normal¨»B«/mi»«mo»§#xA0;«/mo»«mo»=«/mo»«mo»§#xA0;«/mo»«mi mathvariant=¨normal¨»A«/mi»«mo»§#xA0;«/mo»«mo»+«/mo»«mo»§#xA0;«/mo»«mi mathvariant=¨normal¨»V«/mi»«mo»§#xA0;«/mo»«mo»-«/mo»«mo»§#xA0;«/mo»«mn»12«/mn»«/menclose»«mo»§#xA0;«/mo»«mo»(«/mo»«mi»Equa§#xE7;§#xE3;o«/mi»«mo»§#xA0;«/mo»«mn»3«/mn»«mo»)«/mo»«/mrow»«/mstyle»«/math»$

Substituindo a equação 1 nas equações 2 e 3, tem-se:

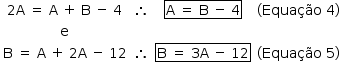
Substituindo a equação 4 na equação 5, chega-se a:

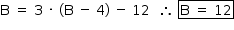
Assim, a urna contém 12 bolas brancas.