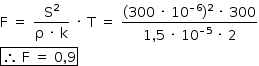Materiais termoelétricos são aqueles com alto potencial de transformar calor em energia elétrica. A capacidade de conversão de calor em eletricidade é quantificada pela grandeza , que é adimensional e função da temperatura T e das propriedades do material: resistividade elétrica ρ, condutividade térmica k, coeficiente Seebeck S. O gráfico a seguir mostra ρ em função de T para certo material termoelétrico. Analisando o gráfico e considerando k = 2,0 W/(m K) × e S = 300 μV/K para esse material, a uma temperatura T = 300 K , conclui-se que a grandeza F desse material a essa temperatura vale
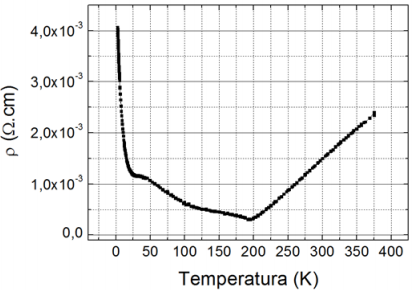
De acordo com o gráfico dado, pode-se identificar a resistividade elétrica para T = 300 K:

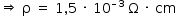
Transformando-se a unidade de Ω · cm para Ω · m, tem-se:
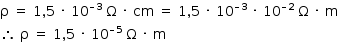
Utilizando-se a expressão apresentada, tem-se: