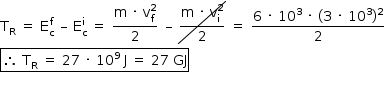Sempre que necessário, use aceleração da gravidade g = 10 m/s2
O primeiro satélite geoestacionário brasileiro foi lançado ao espaço em 2017 e será utilizado para comunicações estratégicas do governo e na ampliação da oferta de comunicação de banda larga. O foguete que levou o satélite ao espaço foi lançado do Centro Espacial de Kourou, na Guiana Francesa. A massa do satélite é constante desde o lançamento até a entrada em órbita e vale m = 6,0 x 103 kg. O módulo de sua velocidade orbital é igual a vor = 3,0 x 103 m/s. Desprezando a velocidade inicial do satélite em razão do movimento de rotação da Terra, o trabalho da força resultante sobre o satélite para levá-lo até a sua órbita é igual a
O trabalho da resultante das forças pode ser obtido a partir do teorema da energia cinética. Sabendo que a massa do satélite é de 6 · 103 kg, que a sua velocidade inicial é nula (desprezando-se a velocidade devido ao movimento de rotação da Terra), e que ele atinge velocidade orbital de 3 · 103 m/s, tem-se: