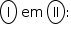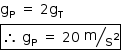Sempre que necessário, use aceleração da gravidade g = 10 m/s2
Recentemente, a agência espacial americana anunciou a descoberta de um planeta a trinta e nove anos-luz da Terra, orbitando uma estrela anã vermelha que faz parte da constelação de Cetus. O novo planeta possui dimensões e massa pouco maiores do que as da Terra e se tornou um dos principais candidatos a abrigar vida fora do sistema solar. Considere este novo planeta esférico com um raio igual a
RP = 2RT e massa MP = 8MT , em que RT e MT são o raio e a massa da Terra, respectivamente. Para planetas esféricos de massa M e raio R , a aceleração da gravidade na superfície do planeta é dada por , em que G é uma constante universal. Assim, considerando a Terra esférica e usando a aceleração da gravidade na sua superfície, o valor da aceleração da gravidade na superfície do novo planeta será de
Na superfície da Terra, a aceleração da gravidade é dada por:
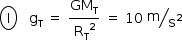
Na superfície do novo planeta, a aceleração da gravidade pode ser calculada substituindo-se MP = 8MT e RP = 2RT, logo:
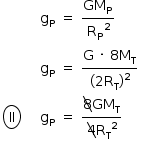
Substituindo a equação