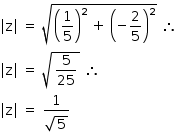Sejam a e b números reais não nulos. Se o número complexo z = a + bi é uma raiz da equação quadrática x2 + bx + a = 0, então
- a
|z| =1/
.
- b
|z| = 1/
.
- c
|z| =
- d
|z| =
Como os coeficientes da equação x2 + bx + a = 0 são reais e o imaginário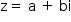 
é uma raiz, então o seu conjugado 
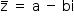também é.
Das relações de Girard para a soma e o produto das raízes de uma equação do 2º grau, tem-se:
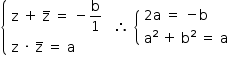
Da primeira equação, tem-se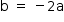 
. Substituindo na segunda, chega-se a:
Logo, o módulo de z é:
