Anglo Resolve

Questão 28

Sejam p(x) e q(x) polinômios com coeficientes reais. Dividindo-se p(x) por q(x), obtêm-se quociente e resto iguais a x² + 1. Nessas condições, é correto afirmar que

a
o grau de p(x) é menor que 5.
b
o grau de q(x) é menor que 3.
c
p(x) tem raízes complexas.
d
q(x) tem raízes reais.

Resolução

Do enunciado, tem-se:

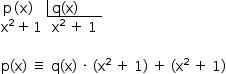
Fatorando p(x), tem-se:

As raízes de p(x) são obtidas de

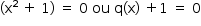
De 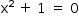, tem-se:

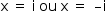, que são raízes imaginárias.

Note-se que, independentemente das raízes de p(x) serem reais ou imaginárias, elas certamente são complexas (pelo teorema fundamental da Álgebra).

Assim, a alternativa C estaria correta de qualquer forma.