No plano cartesiano, sejam C a circunferência de centro na origem e raio r > 0 e s a reta de equação x + 3y = 10. A reta s intercepta a circunferência C em dois pontos distintos se e somente se
Sendo (0,0) o centro da circunferência e x + 3y – 10 = 0 a equação da reta s, para que essa reta intersecte a circunferência em dois pontos distintos, a distância do ponto (0,0) à reta s deve ser menor que a medida r do raio.
Disso,
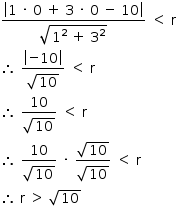
Solução alternativa:
Sejam as equações da circunferência C e reta s, respectivamente:

Substituindo-se II em I, tem-se:

Para que essa equação de 2º grau tenha duas raízes reais distintas, ou seja, para que a reta s intersecte a circunferência C em dois pontos distintos, tem-se:
