Sejam a e b números reais tais que a matriz satisfaz a equação A2 = aA + bl, em que I é a matriz identidade de ordem 2. Logo, o produto ab é igual a
Obtendo-se os valores de a e b, tais que 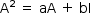
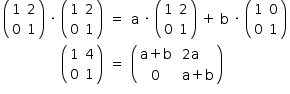
Da igualdade das matrizes, vem:
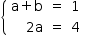
Resolvendo o sistema, obtem-se:
a = 2 e b = –1
Logo, 