Seja x um número real tal que sen x + cos x = 0,2. Logo, | sen x − cos x| é igual a
Do enunciado, tem-se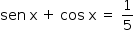 
. Daí, segue que:
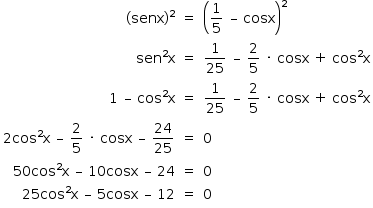
Resolvendo a equação, tem-se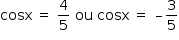 
.
Em ambos os casos,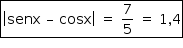 
.
Seja x um número real tal que sen x + cos x = 0,2. Logo, | sen x − cos x| é igual a
Do enunciado, tem-se 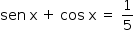. Daí, segue que:
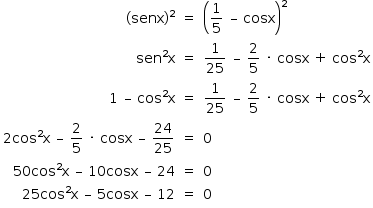
Resolvendo a equação, tem-se .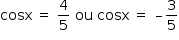
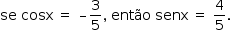
Em ambos os casos, 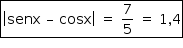.