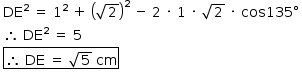Considere que o quadrado ABCD, representado na figura abaixo, tem lados de comprimento de 1 cm, e que C é o ponto médio do segmento AE. Consequentemente, a distância entre os pontos D e E será igual a
- a
cm.
- b
2 cm.
- c
cm.
- d
cm.
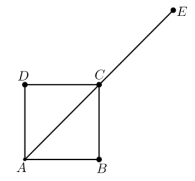
Veja a figura a seguir, em que estão destacadas as medidas dos segmentos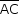 
e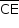 
e dos ângulos 
e 
:
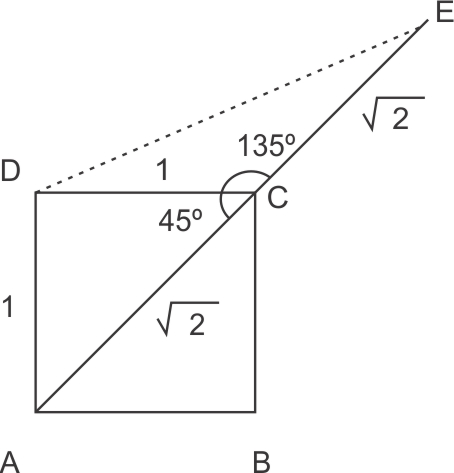
Aplicando o teorema dos cossenos ao triângulo DCE, tem-se:
