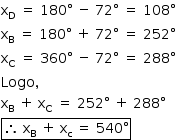A figura indica os gráficos das funções I, II e III. Os pontos A(72º, 0,309), B(xB, –0,309) e C(xC, 0,309) são alguns dos pontos de intersecção dos gráficos.
Nas condições dadas, xB+ xC é igual a
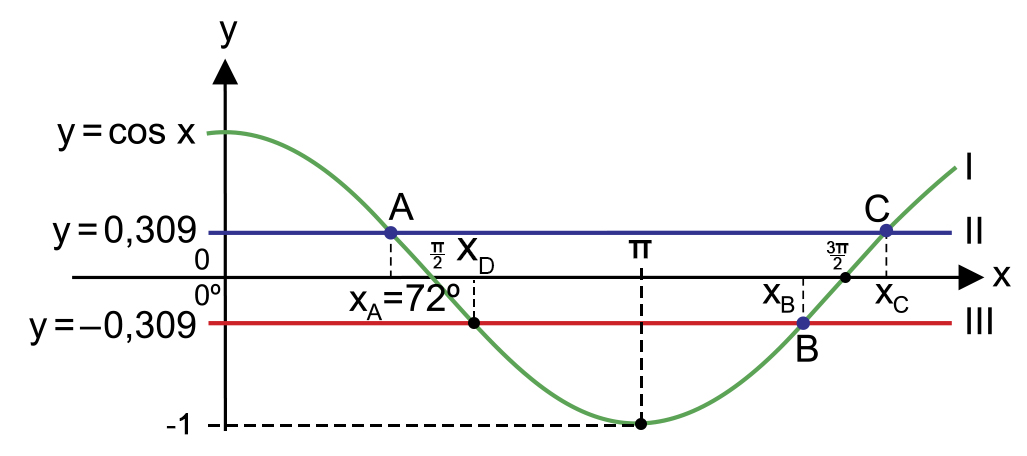
A partir da figura do enunciado, tem-se:
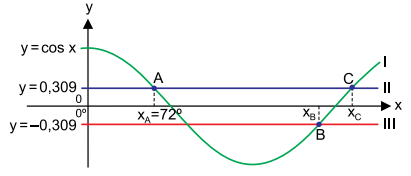
As abscissas dos pontos D, B e C representam os arcos simétricos a 72
nos segundo, terceiro e quarto quadrantes, respectivamente. Disso, tem-se:
