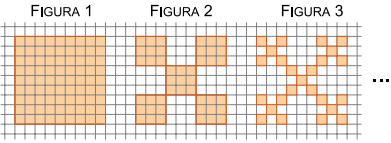
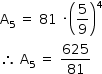A sequência de figuras, desenhadas em uma malha quadriculada, indica as três primeiras etapas de formação de um fractal. Cada quadradinho dessa malha tem área de 1 cm2.
Dado que as áreas das figuras, seguindo o padrão descrito por esse fractal, formam uma progressão geométrica, a área da figura 5, em cm2, será igual a
Sendo A1, A2 e A3 as áreas da figura 1, figura 2 e figura 3, respectivamente, tem-se:
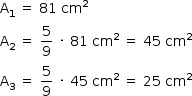
Como as áreas das figuras, seguindo o padrão descrito, formam uma progressão geométrica, a área da figura 5 será dada por: