A figura mostra a trajetória de um projétil lançado obliqua-mente e cinco pontos equidistantes entre si e localizados sobre o solo horizontal. Os pontos e a trajetória do projétil estão em um mesmo plano vertical.
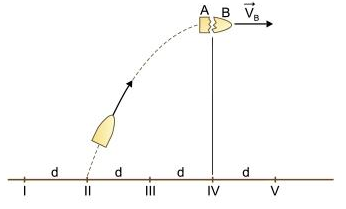
No instante em que atingiu o ponto mais alto da trajetória, o projétil explodiu, dividindo-se em dois fragmentos, A e B, de massas MA e MB, respectivamente, tal que MA = 2MB. Desprezando a resistência do ar e considerando que a velocidade do projétil imediatamente antes da explosão era VH e que, imediatamente após a explosão, o fragmento B adquiriu velocidade VB = 5VH, com mesma direção e sentido de VH, o fragmento A atingiu o solo no ponto
Considerando, no instante da explosão, o sistema mecanicamente isolado:
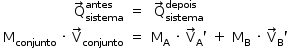
Do enunciado, tem-se:
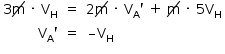
Nota-se, na figura do enunciado, que o projétil parte do ponto II e atinge a altura máxima com velocidade horizontal VH.
Após a explosão, o fragmento A parte com velocidade horizontal –VH, portanto de mesma intensidade e sentido oposto ao projétil antes da explosão.
Uma vez que o alcance independe da massa, o fragmento A atingirá o mesmo ponto de partida, ou seja, o ponto II.