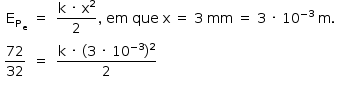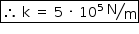Uma minicama elástica é constituída por uma superfície elástica presa a um aro lateral por 32 molas idênticas, como mostra a figura. Quando uma pessoa salta sobre esta minicama, transfere para ela uma quantidade de energia que é absorvida pela superfície elástica e pelas molas.

Considere que, ao saltar sobre uma dessas minicamas, uma pessoa transfira para ela uma quantidade de energia igual a 160 J, que 45% dessa energia seja distribuída igualmente entre as 32 molas e que cada uma delas se distenda 3,0 mm. Nessa situação, a constante elástica de cada mola, em N/m, vale
A quantidade de energia ΔE transferida para as molas é dada por:
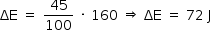
Como são 32 molas, para cada uma tem-se: