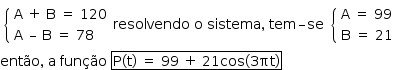Um cientista, em seus estudos para modelar a pressão arterial de uma pessoa, utiliza uma função do tipo P(t) = A + Bcos(kt) em que A, B e K são constantes reais positivas e t representa a variável tempo, medida em segundo. Considere que um batimento cardíaco representa o intervalo de tempo entre duas sucessivas pressões máximas.
Ao analisar um caso específico, o cientista obteve os dados:

A função P(t) obtida, por este cientista, ao analisar o caso específico foi
A função que modela a pressão arterial com A, B e K constantes reais e positivas é P(t) = A + Bcos(kt). Da tabela tem-se que a frequência será: