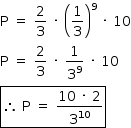Numa avenida existem 10 semáforos. Por causa de uma pane no sistema, os semáforos ficaram sem controle durante uma hora, e fixaram suas luzes unicamente em verde ou vermelho. Os semáforos funcionam de forma independente; a probabilidade de acusar a cor verde é de e a de acusar a cor vermelha é de
. Uma pessoa percorreu a pé toda essa avenida durante o período da pane, observando a cor da luz de cada um desses semáforos.
Qual a probabilidade de que esta pessoa tenha observado exatamente um sinal na cor verde?
Considerem-se os eventos
A: acusar cor verde
B: acusar cor vermelha
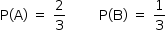
A probabilidade de somente o primeiro semáforo acusar a cor verde é dada por:

Como tem-se 10 semáforos, existem 10 formas de somente um deles acusar a cor verde.
Logo, a probabilidade p pedida é dada por: