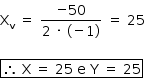Viveiros de lagostas são construídos, por cooperativas locais de pescadores, em formato de prismas reto-retangulares, fixados ao solo e com telas flexíveis de mesma altura, capazes de suportar a corrosão marinha. Para cada viveiro a ser construído, a cooperativa utiliza integralmente 100 metros lineares dessa tela, que é usada apenas nas laterais.

Quais devem ser os valores de X e de Y, em metro, para que a área da base do viveiro seja máxima?
Como é necessário utilizar 100 metros lineares de tela, tem-se:
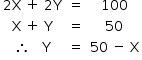
A área da base do viveiro é dada por:
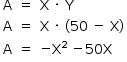
O valor de X para que a área seja máxima é o vértice.