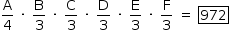O comitê organizador da Copa do Mundo 2014 criou a logomarca da Copa, composta de uma figura plana e o slogan "Juntos num só ritmo", com mãos que se unem formando a taça Fifa. Considere que o comitê organizador resolvesse utilizar todas as cores da bandeira nacional (verde, amarelo, azul e branco) para colorir a logomarca, de forma que regiões vizinhas tenham cores diferentes.

De quantas maneiras diferentes o comitê organizador da Copa poderia pintar a logomarca com as cores citadas?
Da forma como está no enunciado (utilizando todas as quatro cores para colorir a logomarca), a questão não possui alternativa correta, como mostra a resolução a seguir.
Sejam A, B, C, D, E e F cada uma das seis regiões, conforme ilustra a figura abaixo:
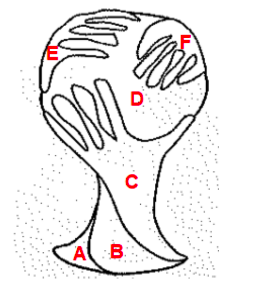
Para que se utilize, obrigatoriamente, as 4 cores há duas situações possíveis:
i. ou há um par de regiões com uma cor, outro par com outra cor e as
duas regiões restantes com as duas cores ainda não utilizadas;
ii. ou há um trio de regiões com a mesma coloração e as três regiões
remanescentes cada uma de uma cor ainda não utilizada.
Nota: Para efeito de resolução, para dizer que a cor usada em X é igual a cor utilizada em Y, usaremos a notação X=Y.
Estudando ambas as situações, temos:
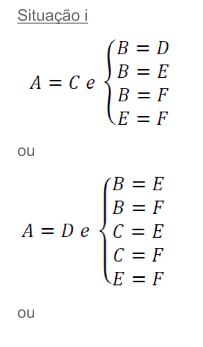
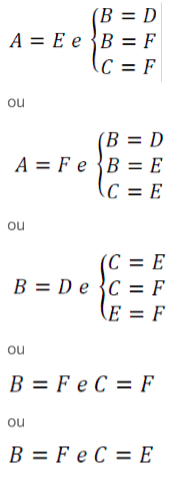
Logo, há 20 configurações possíveis. Para cada uma dela, as maneiras de colorir são iguais. Assim, sem perda de generalidade, calculemos o caso A=C e B=D:
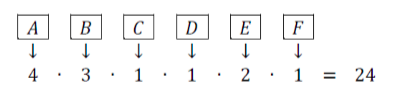


Observação:
Se considerarmos que a questão é apenas "colorir a logomarca utilizando as 4 cores da bandeira", ou seja, sem a obrigatoriedade de as quatro serem utilizadas simultaneamente, tem-se 6 regiões, A, B, C, D, E e F, conforme a figura abaixo.
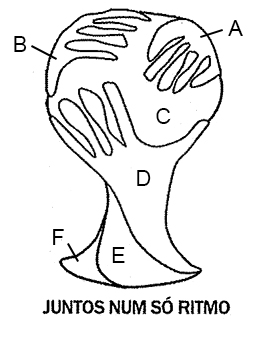
O número de maneiras seria dado por: