A imagem apresentada na figura é uma cópia em preto e branco da tela quadrada intitulada O peixe, de Marcos Pinto, que foi colocada em uma parede para exposição e fixada nos pontos A e B.
Por um problema na fixação de um dos pontos, a tela se desprendeu, girando rente à parede. Após o giro, ela ficou posicionada como ilustrado na figura, formando um ângulo de 45° com a linha do horizonte.
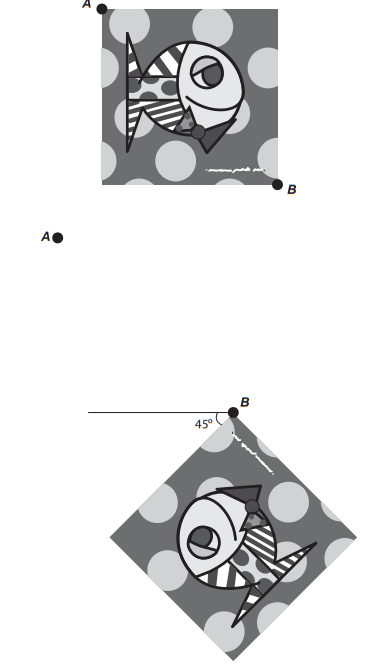
Para recolocar a tela na sua posição original, deve-se girá-la, rente à parede, no menor ângulo possível inferior a 360°.
A forma de recolocara tela na posição original, obedecendo ao que foi estabelecido, é girando-a em um ângulo de
Observe a posição do segmento orientado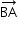 
nas figuras 1 e 2:
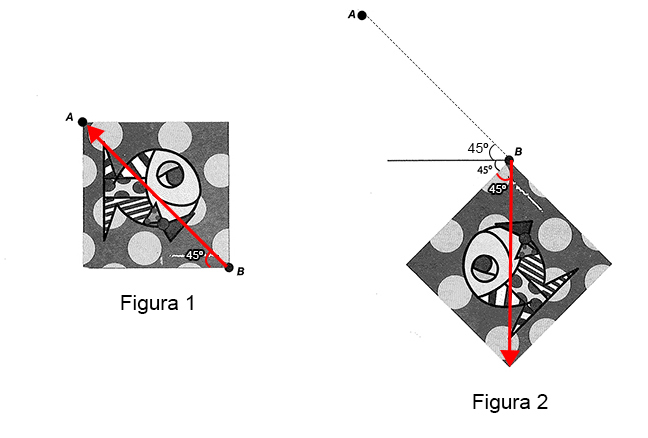
Ao se desprender no ponto A, a tela realiza um giro de 3 · 45° = 135° no sentido anti-horário.
Assim, para recolocá-la na posição original, deve-se girá-la em um ângulo de medida 135° no sentido horário, ou girá-la em um ângulo de medida 360° – 135° = 225° no sentido anti-horário.
Portanto, a menor medida de ângulo possível em que se deve girar a tela, para retornar à posição original, é de 135° no sentido horário.