A figura ilustra uma partida de Campo Minado, o jogo presente em praticamente todo computador pessoal. Quatro quadrados em um tabuleiro 16 x 16 foram abertos, e os números em suas faces indicam quantos dos seus 8 vizinhos contêm minas (a serem evitadas). O número 40 no canto inferior direito é o número total de minas no tabuleiro, cujas posições foram escolhidas ao acaso, de forma uniforme, antes de se abrir qualquer quadrado.
Em sua próxima jogada, o jogador deve escolher dentre os quadrados marcados com as letras P, Q, R, S e T um para abrir, sendo que deve escolher aquele com a menor probabilidade de conter uma mina.
O jogador deverá abrir o quadrado marcado com a letra
Do enunciado, as probabilidades dos quadrados P, Q, S e T conterem uma mina são:
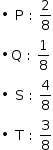
Resta, portanto, analisar o quadrado R.
Como quatro quadrados já foram abertos, eles certamente não contêm minas. Além disso, sabe-se que, se um determinado quadrado indica um número n e tem 8 vizinhos a serem, (8 - n) desses vizinhos não contém minas. Assim, sabe-se que, além dos 4 que já foram abertos, outros (6 + 7 + 4 + 5) também não possuem minas, ou seja, há 4 + 6 + 7 + 4 + 5 = 26 quadrados do tabuleiro que, certamente, não contêm minas e ainda não foram abertos.
Da mesma forma, pode-se concluir que, dos quadrados que ainda não foram abertos, 2 + 1 + 4 + 3 = 10 certamente contêm minas.
Assim, qualquer quadrado que não seja um dos já abertos, nem um dos vizinhos deles, pode conter uma das 40 – 10 = 30 minas restantes. Como são 256 – 26 – 10 = 220 quadrados nessas condições, a probabilidade de que R (que é um desses quadrados) contenha uma mina é:
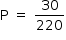
Como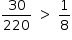 
, o quadrado Q é o que apresenta a menor probabilidade de conter uma mina.