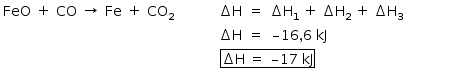O ferro é encontrado na natureza na forma de seus minérios, tais como a hematita (α-Fe203), a magnetita (Fe304) e a wustita (FeO). Na siderurgia, o ferro-gusa é obtido pela fusão de minérios de ferro em altos fornos em condições adequadas. Uma das etapas nesse processo é a formação de monóxido de carbono. O CO (gasoso) é utilizado para reduzir o FeO (sólido), conforme a equação química:
FeO (s) + CO (g) —> Fe (s) + CO2 (g)
Considere as seguintes equações termoquímicas:
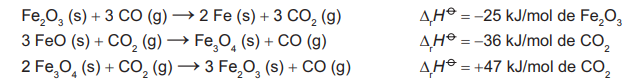
O valor mais próximo de , em kJ/mol de FeO, para a reação indicada do FeO (sólido) com o CO (gasoso) é
Aplicando a Lei de Hess:
Manter e dividir por 2 a equação I
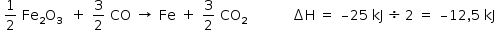
Manter e dividir por 3 a equação II
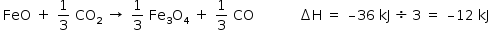
Manter e dividir por 6 a equação III
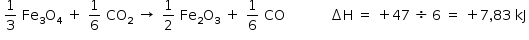
Somando as equações, tem-se: