Óptica da Visão
O olho humano, responsável pela visão, pode distinguir cerca de 10 milhões de cores e é capaz de detectar um único fóton.
É um sistema óptico complexo, formado por vários meios transparentes, além de um sistema fisiológico com inúmeros componentes e todo o conjunto é chamado GLOBO OCULAR. Pela complexidade de se traçar os trajetos dos raios luminosos através desses diferentes meios, convencionou-se representar todos eles por uma única lente convergente biconvexa (o cristalino), de distância focal variável, essa representação é chamada de olho reduzido.
Chama-se Óptica da Visão o estudo das trajetórias dos raios luminosos, através do globo ocular, até a formação de imagens no cérebro. As pessoas que tem visão considerada normal, emetropes, têm a capacidade de conjugar imagens nítidas para objetos situados em média a 25 cm da lente (ponto próximo), por convenção, até distâncias no infinito visual (ponto remoto).
O cristalino é uma lente transparente e flexível, localizada atrás da pupila. Sua distância focal pode ser ajustada para focar objetos em diferentes distâncias, num mecanismo chamado acomodação.
A íris (na figura ao lado) é a área verde/cinza/marrom (castanha), medindo cerca de 12 mm de diâmetro. As outras estruturas visíveis são a pupila(círculo preto no centro) e a esclera (parte branca do olho) ao redor da íris. A córnea está presente, mas não é possível vê-la na foto, por ser transparente. Teoricamente, poderíamos pensar no centro da pupila como sendo o centro da íris.
A pupila é um espaço vazio em forma circular, normalmente preto, definido pela margem interior da íris. Mede de 1,5 mm de diâmetro com muita luz até 8 mm de diâmetro com pouca luz. Sua função é controlar a passagem de luz que chega até a retina. Quando o olho é exposto a níveis de iluminação muito elevados, a pupila se contrai (na verdade a íris dilata), efeito chamado de Pupillary Reflex.
A) Admita a íris da figura recebendo pouca luz. Qual a área da região colorida? (adote π = 3,1)
B) Chamamos de amplitude de acomodação visual a variação da vergência do cristalino de um olho, funcionando como uma lente, capaz de conjugar imagens nítidas para um objeto situado em seu ponto próximo e no seu ponto remoto. Determine, em metros, a distância do ponto próximo para uma pessoa que possua o ponto remoto normal e cuja amplitude de acomodação visual seja de 2,5 di.
a) Considerando a íris como um círculo com 12 mm de diâmetro (R = 6 mm) e a pupila, com pouca luz, um círculo com 8 mm de diâmetro (r = 4 mm), a área pedida é dada por:

b) De acordo com o enunciado e as informações do texto, inicialmente é possível se determinar as vergências do olho no ponto remoto e no ponto próximo:
Ponto remoto:
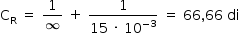
Ponto próximo:
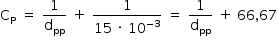
Da definição de amplitude de acomodação, tem-se:
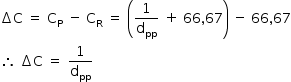
Como, de acordo com o enunciado, a amplitude de acomodação é 2,5 di, tem-se: