• O resto da divisão de um polinômio do segundo grau P pelo binômio ( x + 1) é igual a 3. Dado que P(0) = 6 e P(1) = 5, o valor de P(3) é
Do enunciado, temos que P(x) = ax2 + bx + c. Além disso, temos que P(0) = 6, P(1) = 5 e, pelo teorema do resto, P(–1) = 3. Assim, segue que
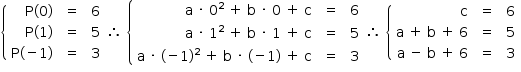
Resolvendo o sistema, temos a = –b, b = 1 e c = 6. Assim, temos que
P(x) = –2x2 + x + 6 e, portanto, P(3) = –2 · 32 + 3 + 6 = –9.