• A função modular f(x) = |ax + b|, a ∈ ℝ*, b ∈ ℝ e a função quadrática g(x) = –0,5x2 + 2x + 6 têm dois pontos em comum, conforme o gráfico.
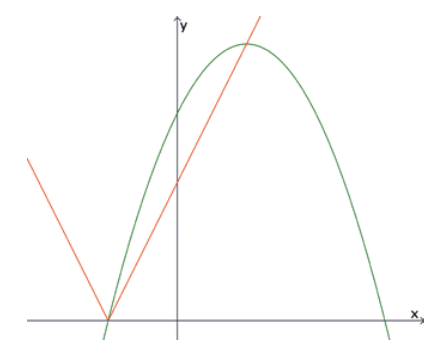
• Um desses pontos corresponde à menor raiz da função g e o outro ponto corresponde ao maior valor dessa função. O produto ab vale
As raízes da função g são obtidas por meio da resolução da equação –0,5x2 + 2x + 6 = 0, cujas raízes são –2 e 6. Logo, a função f(x) intercepta o eixo x no ponto (–2, 0).
As coordenadas do vértice da parábola são dadas por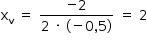 
e yv = g(2) = 8. Assim, temos que o gráfico da função f passa pelos pontos (–2, 0) e (2, 8).
Dado que no intervalo [–2, 8] temos f(x) ≥ 0, vem
Assim, a · b = 2 · 4 = 8.
Obs: Como f(x) = |ax + b|, também poderíamos ter a = –b e b = –4, mas, ainda assim, a · b = 8.