• Um torneio de xadrez terá alunos de 3 escolas. Uma das escolas levará 120 alunos; outra, 180 alunos; e outra, 252 alunos. Esses alunos serão divididos em grupos, de modo que cada grupo tenha representantes das três escolas, e o número de alunos de cada escola seja o mesmo em cada grupo. Dessa maneira, o maior número de grupos que podem ser formados é
Sendo n o maior número de grupos que se pode obter, cada grupo deverá ter:
-
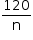alunos da primeira escola, -
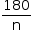alunos da segunda escola e -
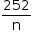alunos da terceira escola.
Nessas condições, n é o máximo divisor comum de 120, 180 e 252.
n = mdc(120, 180, 252)
n = 12.