• Sejam A, B e C subconjuntos do conjunto dos números naturais ℕ = {0, 1, 2, 3, 4,…}, de modo que:
• A é o conjunto dos números de 3 algarismos, todos distintos.
• B é o conjunto dos números que possuem exatamente 1 algarismo 5.
• C é o conjunto dos números pares.
E sejam os conjuntos:
P = A ∩ C
Q = Ac ∩ Bc
R = B Cc
onde a notação Xc indica o conjunto complementar do conjunto X.
São elementos respectivos dos conjuntos P, Q e R os números
1º Modo
Das descrições dos conjuntos no enunciado, concluímos que:
-
AC: conjunto dos números naturais que não tem 3 algarismos ou com que têm 3 algarismos sendo pelo menos dois deles iguais.
-
BC: conjunto dos números naturais que não possuem o algarismo 5 ou que possuem 2 ou mais algarismos iguais a 5.
-
CC: conjunto dos números ímpares.
Assim,
-
P = A ∩ C: conjunto dos números pares com 3 algarismos distintos.
-
Q = AC ∩ BC: conjunto dos números naturais que não tem 3 algarismos ou com que têm 3 algarismos sendo pelo menos dois deles iguais e que não possuem exatamente 1 algarismo 5.
-
R = B ∪ CC: conjunto dos números naturais que possuem exatamente 1 algarismo 5 ou são números ímpares.
Analisando as alternativas, temos:

2º Modo
Note que, sendo X um conjunto qualquer, temos ( ) e (
) e (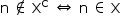 )
)
Analisemos alguns dos números dados nas alternativas.
a) 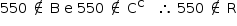
b) 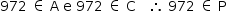

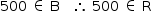
c) 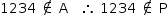
d) 
A alternativa B é a única que apresenta três números que, na ordem dada, são elementos dos conjuntos P, Q e R.