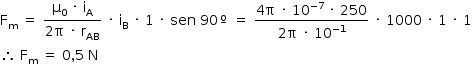• Determine o valor da força magnética, em newtons, entre dois fios metálicos cilíndricos, de mesma resistividade elétrica, retilíneos, paralelos, de comprimentos iguais a 100cm, distanciados em 10cm e com raios de 1mm e 2mm, quando cada um deles for ligado a uma fonte de corrente contínua de diferença de potencial igual a 2,0 V.
Adote: ρ=24 nΩ.m (resistividade elétrica do metal dos fios)
Chamando o fio de raio rA = 1 mm de A e o fio de raio rB = 2 mm de B, pode-se calcular a resistência de cada um aplicando-se a 2a lei de Ohm. Fazendo-se os ajustes de unidades necessários:
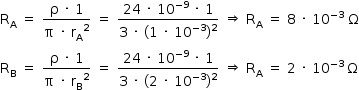
As intensidades das correntes elétricas estabelecidas nos fios são dadas por:
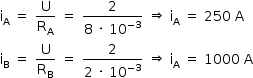
A intensidade da força aplicada pelo fio A sobre o fio B Fm pode ser assim determinada:
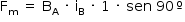
Em que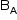 
é a intensidade do campo magnético criado pelo fio A na reta onde está localizado o fio B. Dessa forma, considerando a distância entre os fios igual a rAB:
