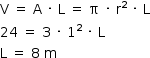• Um caminhão tanque, estacionado sobre um piso plano e horizontal, tem massa de 12 toneladas quando o tanque transportador, internamente cilíndrico, de raio interno 1m, está totalmente vazio. Quando esse tanque está completamente cheio de combustível, ele fica submetido a uma reação normal do solo de 309.600N. Com base nessas informações e nas contidas no gráfico, referentes ao combustível transportado, determine o comprimento interno do tanque cilíndrico, em unidades do SI. Suponha invariável a densidade do combustível em função da temperatura.
Quando o tanque está completamente cheio de combustível, a intensidade da normal aplicada é de 309.600N. Como ele está estacionado em um piso plano e horizontal, a resultante de forças é nula, e a normal apresenta mesma intensidade da força peso.
Sendo assim, a massa total do conjunto caminhão + combustível pode ser calculada da seguinte forma:
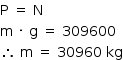
Sabendo que a massa do caminhão vazio é de 12 · t = 12000 kg, a massa do combustível mc é de:
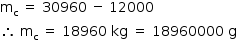
Com as informações do gráfico, podemos calcular a densidade do combustível:
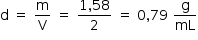
Dessa forma, calculamos o volume V do combustível:
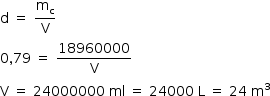
O formato do tanque é cilíndrico, com raio de base r igual a 1 m. Assim, o cálculo do seu comprimento L é dado pela equação: