Quando necessário, adote:
• módulo da aceleração da gravidade: 10 m.s-2
• densidade do ar: 1,2 kg/m3
• calor específico do ar: 0,24 cal.g-1. ºC-1
• 1cal = 4,2 J
• permeabilidade magnética do meio: μ=4.π.10-7 T.m/A
• valor de pi: π=3
• Definimos o intervalo (i) entre dois sons, como sendo o quociente entre suas frequências, i=f2/f1. Quando i=1, dizemos que os sons estão em uníssono; quando i=2, dizemos que o intervalo corresponde a uma oitava acima; quando i=0,5, temos um intervalo correspondente a uma oitava abaixo. Considere uma onda sonora de comprimento de onda igual a 5cm, propagando-se no ar com velocidade de 340m/s. Determine a frequência do som, em hertz, que corresponde a uma oitava abaixo da frequência dessa onda.
De acordo com a equação fundamental da ondulatória, tem-se:
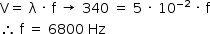
Como a nota musical em uma oitava abaixo possui metade da frequência, ela possuirá frequência de 3400 Hz.