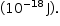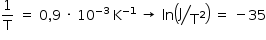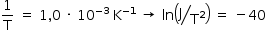Um instrumento importante no estudo de sistemas nanométricos é o microscópio eletrônico. Nos microscópios ópticos, a luz é usada para visualizar a amostra em estudo. Nos microscópios eletrônicos, um feixe de elétrons é usado para estudar a amostra.
a) A vantagem em se usar elétrons é que é possível acelerá-los até energias em que o seu comprimento de onda é menor que o da luz visível, permitindo uma melhor resolução. O comprimento de onda do elétron é dado por λ = h/(2meEc)1/2, em que Ec é a energia cinética do elétron, me~9 × 10−31 kg é a massa do elétron e h~6,6 × 10−34 N∙m∙s é a constante de Planck. Qual é o comprimento de onda do elétron em um microscópio eletrônico em que os elétrons são acelerados, a partir do repouso, por uma diferença de potencial de U = 50 kV? Caso necessário, use a carga do elétron e = 1,6 × 10−19 C.
b) Uma forma usada para gerar elétrons em um microscópio eletrônico é aquecer um filamento, processo denominado efeito termiônico. A densidade de corrente gerada é dada por J = AT2e −Φ⁄(kBT) , em que A é a constante de Richardson, T é a temperatura em kelvin, kB = 1,4 × 10−23 J/K é a constante de Boltzmann e Φ, denominado função trabalho, é a energia necessária para remover um elétron do filamento. A expressão para J pode ser reescrita como ln(J / T2) = ln(A)− (Φ ⁄ kB)(1/T), que é uma equação de uma reta de ln(J/T2) versus (1/T), em que ln(A) é o coeficiente linear e (Φ ⁄ kB) é o coeficiente angular da reta. O gráfico da figura abaixo apresenta dados obtidos do efeito termiônico em um filamento de tungstênio. Qual é a função trabalho do tungstênio medida neste experimento?
a) Aplicando-se o TEC para um elétron:

Como a resultante é a força elétrica Fe, e sabendo-se que o elétron parte do repouso:
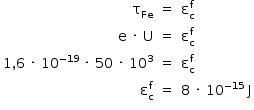
A partir da equação fornecida:
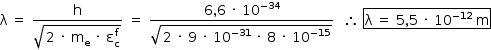
b) Dois pontos que podem ser utilizados com boa aproximação são:
Como o coeficiente angular da reta é igual a 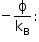
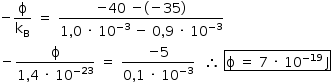
Observação: o gráfico fornecido não possui pontos precisos. Se os pontos acima escolhidos fossem precisos, a reta deveria passar pela ordenada O. Note-se que, para outros pares de pontos, o valor de 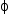 poderia ser diferente, porém sempre da mesma ordem de grandeza
poderia ser diferente, porém sempre da mesma ordem de grandeza