Uma reportagem em revista de divulgação científica apresenta o seguinte título: Pesquisadores estão investigando a possibilidade de combinar hidrogênio com dióxido de carbono para produzir hidrocarbonetos, com alto poder energético, “ricos em energia”. O texto da reportagem explicita melhor o que está no título, ao informar que “em 2014 um grupo de pesquisadores desenvolveu um sistema híbrido que usa bactérias e eletricidade, conjuntamente, em um coletor solar, para gerar hidrogênio a partir da água, e fazer sua reação com dióxido de carbono, para produzir isopropanol”, como representa a equação a seguir.
3 CO2 + 4 H2→ C3H8O + 2,5 O2 ΔrH0 = +862 kJ/mol
a) Considerando que a entalpia padrão de formação da água é -286 kJ/mol, qual é a quantidade de energia que seria utilizada na produção de 1 mol de isopropanol, a partir de água e CO2, da maneira como explica o enunciado acima?
b) Qual seria a energia liberada pela queima de 90 gramas de isopropanol obtido dessa maneira? Considere uma combustão completa e condição padrão.
a) Entalpia de formação da H2O:
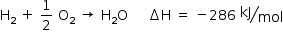
Para obter a reação pedida, precisa-se inverter a equação acima, multiplicar por 4 e somá-la com a equação dada:
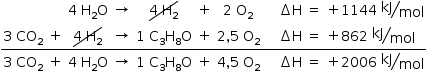
b) Reação de combustão:
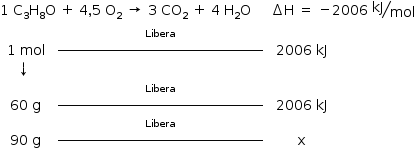
x = 3009 kJ