A figura abaixo exibe três círculos no plano, tangentes dois a dois, com centros em A, B, e C e raios de comprimentos a, b e c, respectivamente.
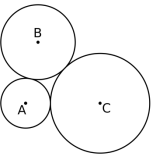
a) Determine os valores de a, b e c, sabendo que a distância entre A e B é de 5 cm, a distância entre A e C é de 6 cm e a distância entre B e C é de 9 cm.
b) Para a = 2 cm e b = 3 cm, determine o valor de c > b de modo que o triângulo de vértices em A, B e C seja retângulo.
a) Do enunciado tem-se a figura abaixo:
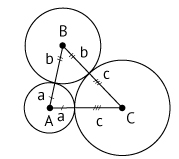
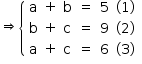
Somando as três equações: 2a + 2b + 2c = 20
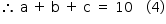
Logo 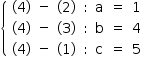
Resposta: a = 1 cm, b = 4 cm e c = 5 cm.
b) Com a = 2 e b = 3, tem-se a figura abaixo:
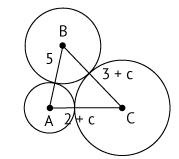
Com c > 3, a hipotenusa é o lado BC. Assim:
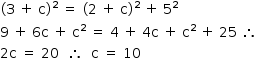
Resposta: c = 10 cm.