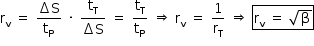Foram identificados, até agora, aproximadamente 4.000 planetas fora do Sistema Solar, dos quais cerca de 10 são provavelmente rochosos e estão na chamada região habitável, isto é, orbitam sua estrela a uma distância compatível com a existência de água líquida, tendo talvez condições adequadas à vida da espécie humana. Um deles, descoberto em 2016, orbita Proxima Centauri, a estrela mais próxima da Terra. A massa, MP, e o raio, RP, desse planeta são diferentes da massa, MT, e do raio, RT, do planeta Terra, por fatores α e β: MP = αMT e RP = βRT
a) Qual seria a relação entre α e β se ambos os planetas tivessem a mesma densidade?
Imagine que você participe da equipe encarregada de projetar o robô C-1PO, que será enviado em uma missão não tripulada a esse planeta. Características do desempenho do robô, quando estiver no planeta, podem ser avaliadas a partir de dados relativos entre o planeta e a Terra.
Nas condições do item a), obtenha, em função de ,
b) a razão entre o valor da aceleração da gravidade, gP, que será sentida por C-1PO na superfície do planeta e o valor da aceleração da gravidade, gT, na superfície da Terra;
c) a razão entre o intervalo de tempo, tP, necessário para que C-1PO dê um passo no planeta e o intervalo de tempo, tT, do passo que ele dá aqui na Terra (considere que cada perna do robô, de comprimento L, faça um movimento como o de um pêndulo simples de mesmo comprimento);
d) a razão entre os módulos das velocidades do robô no planeta, vP, e na Terra, vT.
Note e adote:
A Terra e o planeta são esférico.
O módulo da força gravitacional F entre dois corpos de massas M1 e M2, separados por uma distância r, é dado por , em que G é a constante de gravitação universal.
O período de um pêndulo simples de comprimento L é dado por T = 2π (L/g)1/2, em que g é a aceleração local da gravidade.
Os passos do robô têm o mesmo tamanho na Terra e no planeta
a) 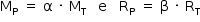
Se os planetas tivessem a mesma densidade, poderíamos escrever:
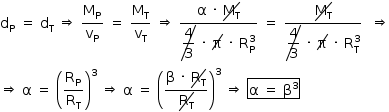
b) As acelerações da gravidade nas superfícies do planeta e da Terra são escritas por 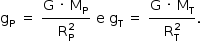
Então:
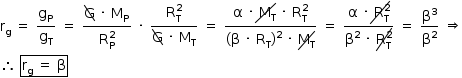
c) O intervalo de tempo necessário para que C-1PO dê um passo no planeta e na Terra corresponde a meio período de oscilação de um pêndulo simples com comprimento igual ao de cada perna do robô. Então:
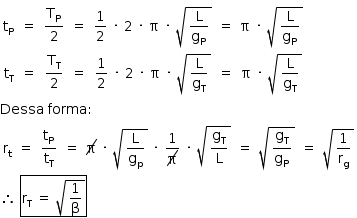
d) 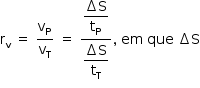 corresponde ao comprimento do passo do robô no planeta ou na Terra. Então:
corresponde ao comprimento do passo do robô no planeta ou na Terra. Então: