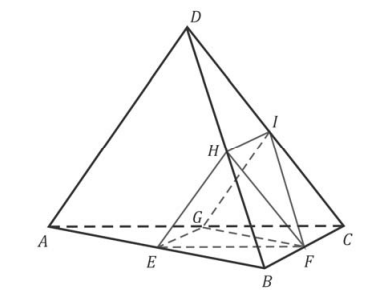
Considere um tetraedro regular ABCD cujas arestas medem 6 cm. Os pontos E, F, G, H e I são os pontos médios das arestas , respectivamente.
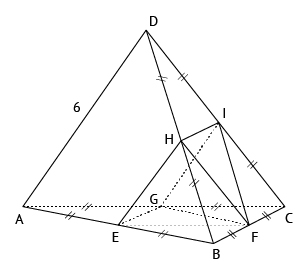
a) Determine a área do triângulo EFH.
b) Calcule a área do quadrilátero EGIH.
c) Determine o volume da pirâmide de vértices E, G, I, H e F, cuja base é o quadrilátero é EGIH.
a)
Os pontos E, F, G, H e I são pontos médios das arestas. Assim,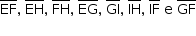 
são bases médias de triângulos equiláteros de lado 6; logo, medem 3. O triângulo EFH é equilátero, de lado ℓ = 3, e sua área é 
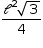, isto é,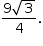 
Resposta: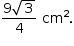 
b) Como duas arestas reversas de um tetraedro regular são ortogonais, 
é ortogonal a 
.
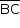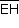é paralela a e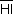 
é paralela a 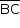; logo, 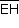é perpendicular a .
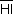Analogamente,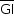 
é perpendicular a 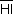e 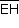é perpendicular a 
.
Portanto, EGIH é um quadrado de lado 3 e sua área vale 32 = 9.
Resposta: 9 cm2.
c)
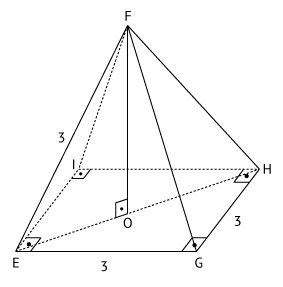
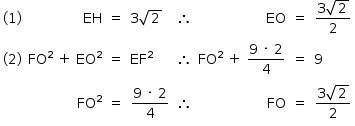
O volume V da pirâmide é
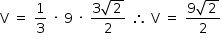
Resposta: 