Um quadriculado é formado por n x n quadrados iguais, conforme ilustrado para n = 2 e n = 3. Cada um desses quadrados será pintado de azul ou de branco. Dizemos que dois quadrados Q1 e Q2 do quadriculado estão conectados se ambos estiverem pintados de azul e se for possível, por meio de movimentos horizontais e verticais entre quadrados adjacentes, sair de Q1 e chegar a Q2 passando apenas por quadrados pintados de azul.
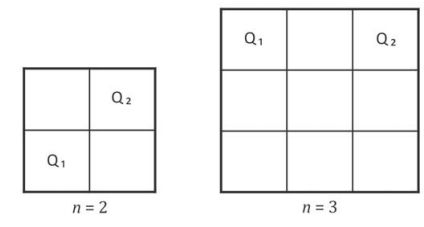
a) Se n = 2, de quantas maneiras distintas será possível pintar o quadriculado de modo que o quadrado Q1 do canto inferior esquerdo esteja conectado ao quadrado Q2 do canto superior direito?
b) Suponha que n = 3 e que o quadrado central esteja pintado de branco. De quantas maneiras distintas será possível pintar o restante do quadriculado de modo que o quadrado Q1 do canto superior esquerdo esteja conectado ao quadrado Q2 do canto superior direito?
c) Suponha que n = 3. De quantas maneiras distintas será possível pintar o quadriculado de modo que o quadrado Q1 do canto superior esquerdo esteja conectado ao quadrado Q2 do canto superior direito?
a) Para que Q1 e Q2 estejam conectados é necessário que pelo menos um dos quadrados remanescentes seja azul. Assim, o número de maneiras distintas de se pintar o quadriculado com tal restrição é:
Total (sem restrição) — Casos desfavoráveis (ambos brancos)
2 · 2 — 1 · 1
= 4 – 1
= 3
Resposta: Há 3 maneiras distintas.
b) Há 2 configurações possíveis:

Na configuração I há 32 maneiras de pintar os quadrados remanescentes.
Na configuração II há apenas 1 maneira.
Assim, há 33 maneiras.
Resposta: Há 33 maneiras.
c) O item b é um caso particular do item c. Avaliemos os casos não contemplados no item anterior.
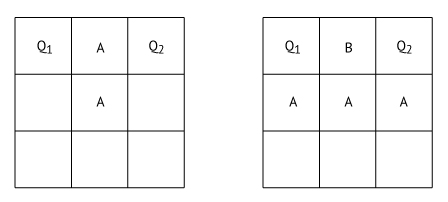
No item anterior há 33 maneiras.
Na primeira configuração acima há 25 = 32 maneiras.
Na segunda configuração acima há 23 = 8 maneiras.
Assim, há 33 + 32 + 8 = 73 maneiras.
Resposta: Há 73 maneiras.