Considere uma folha de papel retangular com lados 20 cm e 16 cm. Após remover um quadrado de lado x cm de cada um dos cantos da folha, foram feitas 4 dobras para construir uma caixa (sem tampa) em forma de paralelepípedo reto-retângulo com altura x cm. As linhas tracejadas na figura indicam onde as dobras foram feitas.
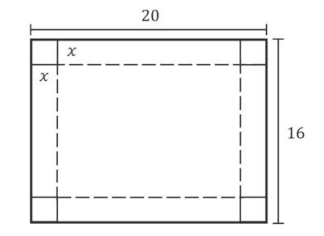
a) Expresse o volume da caixa em função de x.
b) Determine o conjunto dos valores de x para os quais o volume da caixa é maior ou igual a 384 cm3.
a)
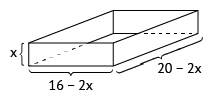
A área da base é (16 – 2x)(20 – 2x) cm2, ou seja, 4(8 – x)(10 – x) cm2. Como a altura é x cm, o volume da caixa é dado por 4x(8 – x)(10 – x) cm3, com 0 < x < 8.
Resposta: 4x(8 – x)(10 – x) cm3.
b) De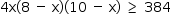 
, tem-se:
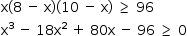
Por uma pesquisa de raízes racionais, pode-se concluir que 2 é um zero do polinômio.
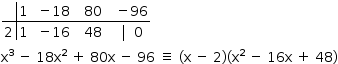
Os zeros de x2 – 16x + 48 são 4 e 12.
Logo,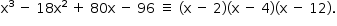 
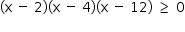
Com a condição 0 < x < 8, conclui-se que o volume da caixa é maior ou igual a 384 cm3 se, e somente se,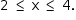 
Resposta: [2, 4].