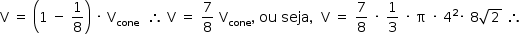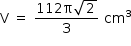Um cone circular reto de geratriz medindo 12 cm e raio da base medindo 4 cm foi seccionado por um plano paralelo à sua base, gerando um tronco de cone, como mostra a figura 1. A figura 2 mostra a planificação da superfície lateral S desse tronco de cone, obtido após a secção.
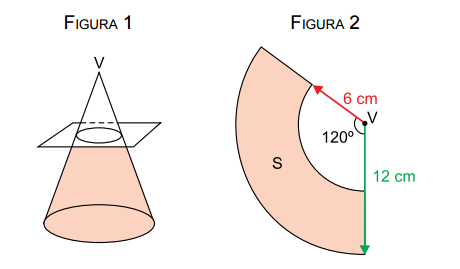
Calcule a área e o perímetro da superfície S. Calcule o volume do tronco de cone indicado na figura 1.
Da figura 2, tem-se que:
- A área A da superfície S é:
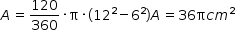
- O perímetro P da superfície S é:
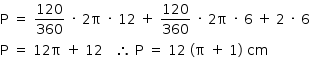
- Da figura 1, tem-se que a razão de semelhança entre os triângulos VCD e VAB é
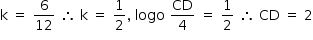
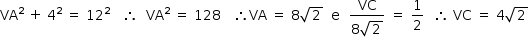
- Assim, o volume V do tronco de cone é:
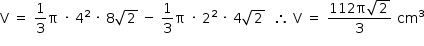
Obs.:
Como a razão de semelhança entre os triângulos VCD e VAB é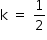 
, a razão entre os volumes do cone menor e do cone maior é 
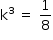, logo, o volume do tronco é 
