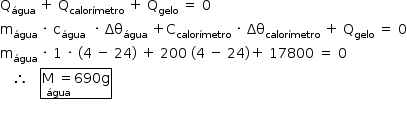Um bloco de gelo de massa 200 g, inicialmente à temperatura de –10 ºC, foi mergulhado em um recipiente de capacidade térmica 200 cal/ºC contendo água líquida a 24 ºC. Após determinado intervalo de tempo, esse sistema entrou em equilíbrio térmico à temperatura de 4 ºC.
O gráfico mostra como variou a temperatura apenas do gelo, desde sua imersão no recipiente até ser atingido o equilíbrio térmico.
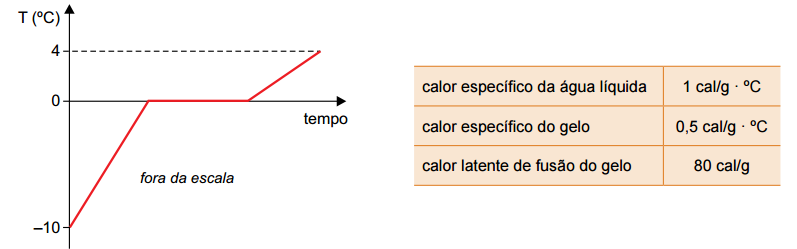
Considerando as informações contidas no gráfico e na tabela, que o experimento foi realizado ao nível do mar e desprezando as perdas de calor para o ambiente, calcule a quantidade de calor absorvido pelo bloco de gelo, em calorias, desde que foi imerso na água até ser atingido o equilíbrio térmico, e calcule a massa de água líquida contida no recipiente, em gramas, antes da imersão do bloco gelo.
A partir do gráfico, a quantidade de calor (Q) absorvida pelo gelo pode ser obtida como se segue:
![«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨14px¨»«msub»«mi mathvariant=¨normal¨»Q«/mi»«mi»total«/mi»«/msub»«mo»§#xA0;«/mo»«mo»=«/mo»«mo»§#xA0;«/mo»«msub»«mi mathvariant=¨normal¨»m«/mi»«mi»gelo«/mi»«/msub»«mo»§#xA0;«/mo»«mo»§#xB7;«/mo»«mo»§#xA0;«/mo»«msub»«mi mathvariant=¨normal¨»c«/mi»«mi»gelo«/mi»«/msub»«mo»§#xA0;«/mo»«mo»§#xB7;«/mo»«mo»§#xA0;«/mo»«msub»«mi»§#x394;§#x3B8;«/mi»«mi»gelo«/mi»«/msub»«mo»§#xA0;«/mo»«mo»+«/mo»«mo»§#xA0;«/mo»«msub»«mi mathvariant=¨normal¨»m«/mi»«mi»gelo«/mi»«/msub»«mo»§#xA0;«/mo»«mo»§#xB7;«/mo»«mo»§#xA0;«/mo»«msub»«mi mathvariant=¨normal¨»L«/mi»«mi»fus§#xE3;o«/mi»«/msub»«mo»§#xA0;«/mo»«mo»+«/mo»«mo»§#xA0;«/mo»«msub»«mi mathvariant=¨normal¨»m«/mi»«mi»gelo«/mi»«/msub»«mo»§#xA0;«/mo»«mo»§#xB7;«/mo»«mo»§#xA0;«/mo»«msub»«mi mathvariant=¨normal¨»c«/mi»«mi»§#xE1;gua«/mi»«/msub»«mo»§#xA0;«/mo»«mo»§#xB7;«/mo»«mo»§#xA0;«/mo»«msub»«mi»§#x394;§#x3B8;«/mi»«mi»§#xE1;gua«/mi»«/msub»«mspace linebreak=¨newline¨/»«msub»«mi mathvariant=¨normal¨»Q«/mi»«mi»total«/mi»«/msub»«mo»§#xA0;«/mo»«mo»=«/mo»«mo»§#xA0;«/mo»«mn»200«/mn»«mo»§#xA0;«/mo»«mo»§#xB7;«/mo»«mo»§#xA0;«/mo»«mn»0«/mn»«mo»,«/mo»«mn»5«/mn»«mo»§#xA0;«/mo»«mfenced open=¨[¨ close=¨]¨»«mrow»«mn»0«/mn»«mo»§#xA0;«/mo»«mo»-«/mo»«mo»§#xA0;«/mo»«mfenced»«mrow»«mo»-«/mo»«mn»10«/mn»«/mrow»«/mfenced»«/mrow»«/mfenced»«mo»§#xA0;«/mo»«mo»+«/mo»«mo»§#xA0;«/mo»«mn»200«/mn»«mo»§#xA0;«/mo»«mo»§#xB7;«/mo»«mo»§#xA0;«/mo»«mn»80«/mn»«mo»§#xA0;«/mo»«mo»+«/mo»«mo»§#xA0;«/mo»«mn»200«/mn»«mo»§#xA0;«/mo»«mo»§#xB7;«/mo»«mo»§#xA0;«/mo»«mn»1«/mn»«mo»§#xA0;«/mo»«mfenced»«mrow»«mn»4«/mn»«mo»§#xA0;«/mo»«mo»-«/mo»«mo»§#xA0;«/mo»«mn»0«/mn»«/mrow»«/mfenced»«mspace linebreak=¨newline¨/»«mo»§#x2234;«/mo»«mo»§#xA0;«/mo»«menclose notation=¨box¨»«msub»«mi mathvariant=¨normal¨»Q«/mi»«mi»total«/mi»«/msub»«mo»§#xA0;«/mo»«mo»=«/mo»«mo»§#xA0;«/mo»«mn»17800«/mn»«mo»§#xA0;«/mo»«mi»cal«/mi»«/menclose»«/mstyle»«/math»](https://anglo.plurall.net/sites/all/libraries/ckeditor//plugins/ckeditor_wiris/integration/showimage.php?formula=9ccf5bcc52ce46e2e1de053a39895dec.png)
Considerando-se o sistema termicamente isolado, tem-se: