Em um experimento, uma população inicial de 100 bactérias dobra a cada 3 horas. Sendo y o número de bactérias após x horas, segue que 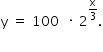
a) Depois de um certo número de horas a partir do início do experimento, a população de bactérias atingiu 1677721600. Calcule esse número de horas. (dado: 16777216 = 2563)
b) Sabendo-se que da 45a para a 48a hora o número de bactérias aumentou de 100 · 2k , calcule o valor de k.
a)
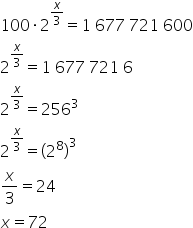
Resposta: x = 72
b)
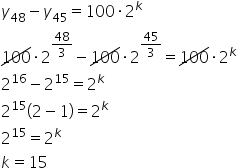
Resposta: k = 15