Os pontos T e U deslocam-se sobre retas paralelas r1 e r2 de tal forma que 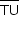 passe sempre pelo centro C de um quadrado PQRS, de lado 2, e forme um ângulo de medida α com r1, conforme indica, como exemplo, a sequência de cinco figuras.
passe sempre pelo centro C de um quadrado PQRS, de lado 2, e forme um ângulo de medida α com r1, conforme indica, como exemplo, a sequência de cinco figuras.
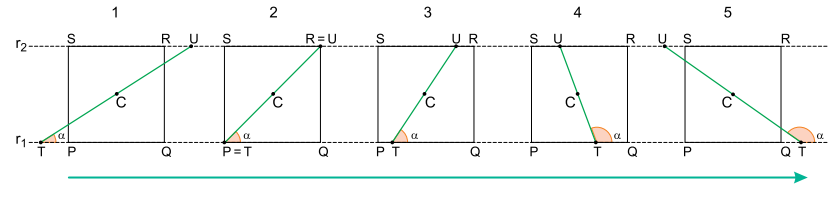
a) Calcule as medidas de nas situações em que α = 45° e α = 90°.
b) Denotando TU por y, determine y em função de α e o respectivo domínio dessa função no intervalo de α em que a posição de T varia de P até Q.
a)
Considere as figuras abaixo:
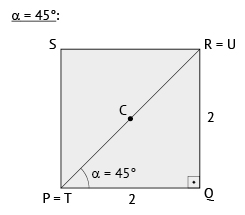
- quando
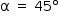 , tem-se que
, tem-se que 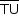 é uma diagonal do quadrado PQRS e, portanto, mede
é uma diagonal do quadrado PQRS e, portanto, mede 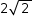 ;
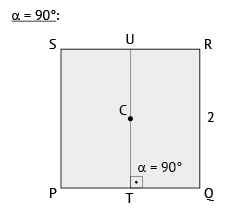
; - quando
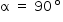 , tem-se que
, tem-se que 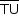 é um segmento paralelo aos lados
é um segmento paralelo aos lados 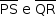 do quadrado, cuja medida é igual à medida do lado do quadrado, ou seja, 2.
do quadrado, cuja medida é igual à medida do lado do quadrado, ou seja, 2.
Resposta: 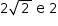
b)
Como a distância entre r1 e r2 vale 2, tem-se a figura:
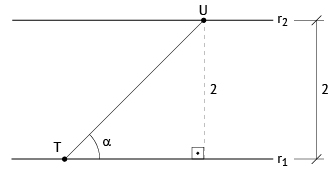
No triângulo retângulo da figura, tem-se:
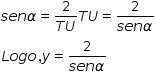
Note que, quando T = P, tem-se 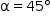 e, quando T = Q, tem-se
e, quando T = Q, tem-se 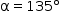 . Ainda, para cada ponto U do segmento
. Ainda, para cada ponto U do segmento 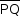 , existe um valor de
, existe um valor de 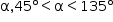 , tal que U = T. Logo, o domínio de
, tal que U = T. Logo, o domínio de 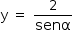 , quando T percorre o segmento
, quando T percorre o segmento 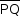 , é dado pelo intervalo
, é dado pelo intervalo ![«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨14px¨»«mrow»«mfenced open=¨[¨ close=¨]¨»«mrow»«mfrac»«mi mathvariant=¨normal¨»§#x3C0;«/mi»«mn»4«/mn»«/mfrac»«mo»§#xA0;«/mo»«mo»,«/mo»«mo»§#xA0;«/mo»«mfrac»«mrow»«mn»3«/mn»«mi mathvariant=¨normal¨»§#x3C0;«/mi»«/mrow»«mn»4«/mn»«/mfrac»«/mrow»«/mfenced»«mo».«/mo»«/mrow»«/mstyle»«/math»](https://anglo.plurall.net/sites/all/libraries/ckeditor//plugins/ckeditor_wiris/integration/showimage.php?formula=e94421bb61092f0cdace05189605b0bd.png)
Resposta: ![«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨14px¨»«mi mathvariant=¨normal¨»y«/mi»«mo»§#xA0;«/mo»«mo»=«/mo»«mo»§#xA0;«/mo»«mfrac»«mn»2«/mn»«mi»sen§#x3B1;«/mi»«/mfrac»«mo»;«/mo»«mo»§#xA0;«/mo»«mi»Dom§#xED;nio«/mi»«mo»:«/mo»«mo»§#xA0;«/mo»«mfenced open=¨[¨ close=¨]¨»«mrow»«mfrac»«mi mathvariant=¨normal¨»§#x3C0;«/mi»«mn»4«/mn»«/mfrac»«mo»,«/mo»«mo»§#xA0;«/mo»«mfrac»«mrow»«mn»3«/mn»«mi mathvariant=¨normal¨»§#x3C0;«/mi»«/mrow»«mn»4«/mn»«/mfrac»«/mrow»«/mfenced»«/mstyle»«/math»](https://anglo.plurall.net/sites/all/libraries/ckeditor//plugins/ckeditor_wiris/integration/showimage.php?formula=812e086a7bbfc5a5828985fedcc250ed.png)