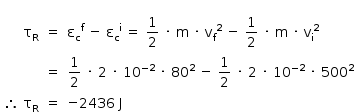Em um teste realizado na investigação de um crime, um projétil de massa 20 g é disparado horizontalmente contra um saco de areia apoiado, em repouso, sobre um carrinho que, também em repouso, está apoiado sobre uma superfície horizontal na qual pode mover-se livre de atrito. O projétil atravessa o saco perpendicularmente aos eixos das rodas do carrinho, e sai com velocidade menor que a inicial, enquanto o sistema formado pelo saco de areia e pelo carrinho, que totaliza 100 kg, sai do repouso com velocidade de módulo v.

O gráfico representa a variação da velocidade escalar do projétil, vP, em função do tempo, nesse teste.

Calcule:
a) o módulo da velocidade v, em m/s, adquirida pelo sistema formado pelo saco de areia e pelo carrinho imediatamente após o saco ter sido atravessado pelo projétil.
b) o trabalho, em joules, realizado pela resultante das forças que atuaram sobre o projétil no intervalo de tempo em que ele atravessou o saco de areia.
a) Na situação descrita no enunciado, o sistema formado por projétil, saco de areia e carrinho é isolado. Assim:
Qsist = Q'sist
mp · Vp = mc · V'c + ms · V's + mp · V'p
De acordo com o enunciado, as velocidades do carrinho e do saco são iguais e apresentam a mesma intensidade V.
mp · Vp = (mc + ms) · V + mp · V'p
2 · 10-2 · 500 = (100) · v + 2 · 10-2 · 80
V = 8,4 · 10-2 m/s
b) Aplicando o teorema da energia cinética para o projétil: