Certo produto utilizado como “tira-ferrugem” contém solução aquosa de ácido oxálico, H2 C2 O4, a 2% (m/V). O ácido oxálico é um ácido diprótico e em suas soluções aquosas ocorrem duas reações de dissociação simultâneas, representadas pelas seguintes equações químicas:
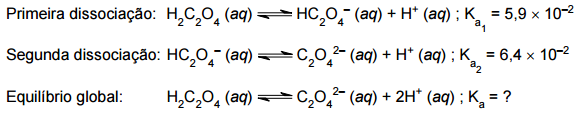
a) Expresse a concentração de ácido oxálico no produto em g/L e em mol/L.
b) Escreva a expressão da constante Ka do equilíbrio global e calcule seu valor numérico a partir das constantes Ka1 e Ka2.
a) A concentração da solução aquosa de ácido oxálico corresponde a 2% (m/V). Assim:

Convertendo-se a massa do ácido para n de mol, tem-se:
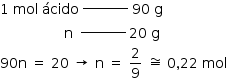
Assim, como esses 0,22 mol estão para 1 L de solução, a concentração da solução corresponde a 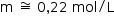
b) A partir das equações fornecidas, tem-se:
Equilíbrio Global: 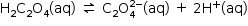
![«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨14px¨»«mrow»«mi»Ka«/mi»«mo»§#xA0;«/mo»«mo»=«/mo»«mo»§#xA0;«/mo»«mfrac»«mrow»«msup»«mfenced open=¨[¨ close=¨]¨»«msup»«mi mathvariant=¨normal¨»H«/mi»«mo»+«/mo»«/msup»«/mfenced»«mn»2«/mn»«/msup»«mo»§#xA0;«/mo»«mo»§#xB7;«/mo»«mo»§#xA0;«/mo»«mfenced open=¨[¨ close=¨]¨»«mrow»«msub»«mi mathvariant=¨normal¨»C«/mi»«mn»2«/mn»«/msub»«msubsup»«mi mathvariant=¨normal¨»O«/mi»«mn»4«/mn»«mrow»«mn»2«/mn»«mo»-«/mo»«/mrow»«/msubsup»«/mrow»«/mfenced»«/mrow»«mfenced open=¨[¨ close=¨]¨»«mrow»«msub»«mi mathvariant=¨normal¨»H«/mi»«mn»2«/mn»«/msub»«msub»«mi mathvariant=¨normal¨»C«/mi»«mn»2«/mn»«/msub»«msub»«mi mathvariant=¨normal¨»O«/mi»«mn»4«/mn»«/msub»«/mrow»«/mfenced»«/mfrac»«/mrow»«/mstyle»«/math»](https://anglo.plurall.net/sites/all/libraries/ckeditor//plugins/ckeditor_wiris/integration/showimage.php?formula=47089d74124bb773094d867cdef52f4d.png)
A partir das constantes Ka1 e Ka2, tem-se: