Chama-se solução trivial de um sistema linear aquela em que todos os valores das incógnitas são nulos.
O sistema linear, nas incógnitas x, y e z: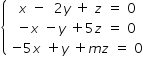
Primeiro, observe que o sistema dado é homogêneo e, portanto, admite pelo menos a solução trivial. Assim, o sistema pode admitir apenas a solução trivial, se for possível e determinado, ou a trivial e infinitas outras, se for possível e indeterminado.
Para analisar cada caso, calcule-se o determinante formado pelos coeficientes das incógnitas:
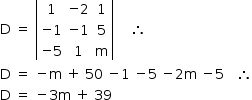
Como D = 0 apenas para m = 13 , temos que, se m ≠ 13, então o sistema é possível e determinado e, portanto, admite apenas a solução trivial.
Logo, se m = 13, o sistema é possível e indeterminado e, portanto, admite outras soluções além da trivial.