Uma matriz A de ordem 2 transmite uma palavra de 4 letras em que cada elemento da matriz representa uma letra do alfabeto.
A fim de dificultar a leitura da palavra, por se tratar de informação secreta, a matriz A é multiplicada pela matriz ![«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨14px¨»«mrow»«mi»B«/mi»«mo»§#xA0;«/mo»«mo»=«/mo»«mo»§#xA0;«/mo»«mfenced open=¨[¨ close=¨]¨»«mtable»«mtr»«mtd»«mn»3«/mn»«/mtd»«mtd»«mo»-«/mo»«mn»1«/mn»«/mtd»«/mtr»«mtr»«mtd»«mo»-«/mo»«mn»5«/mn»«/mtd»«mtd»«mn»2«/mn»«/mtd»«/mtr»«/mtable»«/mfenced»«/mrow»«/mstyle»«/math»](https://anglo.plurall.net/sites/all/libraries/ckeditor//plugins/ckeditor_wiris/integration/showimage.php?formula=41eae3976b25c7a514f417c0ff82fd70.png) obtendo-se a matriz codificada B.A.
obtendo-se a matriz codificada B.A.
Sabendo que a matriz B.A é igual a ![«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨14px¨»«mfenced open=¨[¨ close=¨]¨»«mtable»«mtr»«mtd»«mo»-«/mo»«mn»10«/mn»«/mtd»«mtd»«mn»27«/mn»«/mtd»«/mtr»«mtr»«mtd»«mn»21«/mn»«/mtd»«mtd»«mo»-«/mo»«mn»39«/mn»«/mtd»«/mtr»«/mtable»«/mfenced»«/mstyle»«/math»](https://anglo.plurall.net/sites/all/libraries/ckeditor//plugins/ckeditor_wiris/integration/showimage.php?formula=c42e2a787addca5e1d6443a4cb34c06b.png) , podemos afirmar que a soma dos elementos da matriz A é:
, podemos afirmar que a soma dos elementos da matriz A é:
Seja a matriz ![«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨14px¨»«mrow»«mi mathvariant=¨normal¨»A«/mi»«mo»§#xA0;«/mo»«mo»=«/mo»«mo»§#xA0;«/mo»«mfenced open=¨[¨ close=¨]¨»«mtable»«mtr»«mtd»«mi mathvariant=¨normal¨»a«/mi»«/mtd»«mtd»«mi mathvariant=¨normal¨»b«/mi»«/mtd»«/mtr»«mtr»«mtd»«mi mathvariant=¨normal¨»c«/mi»«/mtd»«mtd»«mi mathvariant=¨normal¨»d«/mi»«/mtd»«/mtr»«/mtable»«/mfenced»«mo».«/mo»«/mrow»«/mstyle»«/math»](https://anglo.plurall.net/sites/all/libraries/ckeditor//plugins/ckeditor_wiris/integration/showimage.php?formula=18dcbd6717779533c3b03f96aedab48e.png) .
.
Tem-se:
![«math style=¨font-family:Tahoma¨ xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mstyle mathsize=¨14px¨»«mrow»«mfenced open=¨[¨ close=¨]¨»«mtable»«mtr»«mtd»«mn»3«/mn»«/mtd»«mtd»«mo»-«/mo»«mn»1«/mn»«/mtd»«/mtr»«mtr»«mtd»«mo»-«/mo»«mn»5«/mn»«/mtd»«mtd»«mn»2«/mn»«/mtd»«/mtr»«/mtable»«/mfenced»«mo»§#xA0;«/mo»«mo»§#xB7;«/mo»«mo»§#xA0;«/mo»«mfenced open=¨[¨ close=¨]¨»«mtable»«mtr»«mtd»«mi mathvariant=¨normal¨»a«/mi»«/mtd»«mtd»«mi mathvariant=¨normal¨»b«/mi»«/mtd»«/mtr»«mtr»«mtd»«mi mathvariant=¨normal¨»c«/mi»«/mtd»«mtd»«mi mathvariant=¨normal¨»d«/mi»«/mtd»«/mtr»«/mtable»«/mfenced»«mo»§#xA0;«/mo»«mo»=«/mo»«mo»§#xA0;«/mo»«mfenced open=¨[¨ close=¨]¨»«mtable»«mtr»«mtd»«mo»-«/mo»«mn»10«/mn»«/mtd»«mtd»«mn»27«/mn»«/mtd»«/mtr»«mtr»«mtd»«mn»21«/mn»«/mtd»«mtd»«mo»-«/mo»«mn»39«/mn»«/mtd»«/mtr»«/mtable»«/mfenced»«mspace linebreak=¨newline¨/»«mfenced open=¨[¨ close=¨]¨»«mtable»«mtr»«mtd»«mn»3«/mn»«mi mathvariant=¨normal¨»a«/mi»«mo»§#xA0;«/mo»«mo»-«/mo»«mo»§#xA0;«/mo»«mi mathvariant=¨normal¨»c«/mi»«/mtd»«mtd»«mn»3«/mn»«mi mathvariant=¨normal¨»b«/mi»«mo»§#xA0;«/mo»«mo»-«/mo»«mo»§#xA0;«/mo»«mi mathvariant=¨normal¨»d«/mi»«/mtd»«/mtr»«mtr»«mtd»«mo»-«/mo»«mn»5«/mn»«mi mathvariant=¨normal¨»a«/mi»«mo»§#xA0;«/mo»«mo»+«/mo»«mo»§#xA0;«/mo»«mn»2«/mn»«mi mathvariant=¨normal¨»c«/mi»«/mtd»«mtd»«mo»-«/mo»«mn»5«/mn»«mi mathvariant=¨normal¨»b«/mi»«mo»§#xA0;«/mo»«mo»+«/mo»«mo»§#xA0;«/mo»«mn»2«/mn»«mi mathvariant=¨normal¨»d«/mi»«/mtd»«/mtr»«/mtable»«/mfenced»«mo»§#xA0;«/mo»«mo»=«/mo»«mo»§#xA0;«/mo»«mfenced open=¨[¨ close=¨]¨»«mtable»«mtr»«mtd»«mo»-«/mo»«mn»10«/mn»«/mtd»«mtd»«mn»27«/mn»«/mtd»«/mtr»«mtr»«mtd»«mn»21«/mn»«/mtd»«mtd»«mo»-«/mo»«mn»39«/mn»«/mtd»«/mtr»«/mtable»«/mfenced»«/mrow»«/mstyle»«/math»](https://anglo.plurall.net/sites/all/libraries/ckeditor//plugins/ckeditor_wiris/integration/showimage.php?formula=e5a9a0c298375de682c4d974cc9b23d4.png)
A partir da igualdade matricial acima, tem-se os seguintes sistemas:
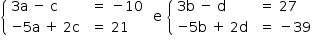
Resolvendo os sistemas, obtêm-se a = 1, b = 15, c = 13 e d = 18.
Logo, a soma dos elementos da matriz A é 1 + 15 + 13 + 18 = 47.